用GeoGebra制作数学动态课件2:两种构造动态对象的方式

1637年,笛卡尔发表了《几何学》,创立了直角坐标系。他用平面上的一点到两条固定直线的距离来确定点的位置,用坐标来描述空间上的点。笛卡尔提出了变数的概念,他进而又创立了解析几何学,表明了几何问题不仅可以归结成为代数形式,而且可以通过代数变换来实现发现几何性质,证明几何性质。解析几何的出现,把相互对立着的“数”与“形”统一了起来,使几何曲线与代数方程相结合。解析几何的创立也为微积分的创立奠定了基础,从而开拓了变量数学的广阔领域。
几何也就被赋予了“代数”的含义。而使用GeoGebra数学构图主要是用解析几何的原理来构造动态的几何对象,使用GeoGebra软件构图也能充分体现解析几何的内涵。
如:使用GeoGebra 构造的“任意三角形”,其顶点可以移动,保持三角形在动态中保持了其“任意”的特性,故称为动态对象。
在GeoGebra 中构建数学对象,可以使用“工具方式”或者“指令方式”实现。“工具方式”就是鼠标点取工具栏工具图标,然后,在绘图区域中构造对象。“指令方式”就是在“指令栏”(GeoGebra6和网页版在代数区也集成了指令输入功能)输入构造对象的指令,实现在“代数区”显示对象的代数表达式,在“绘图区”显示对象的构图。
下面以构造线段AB 为例介绍两种方式。
工具方式:首先,使用“点”工具,在绘图区单击鼠标左键,构造两个点A、B。使用“线段”工具,分别单击点A 和点B,构造线段AB。此时,在“绘图区”出现线段f,在“代数区”出现线段AB 的标签f 和长度等信息。
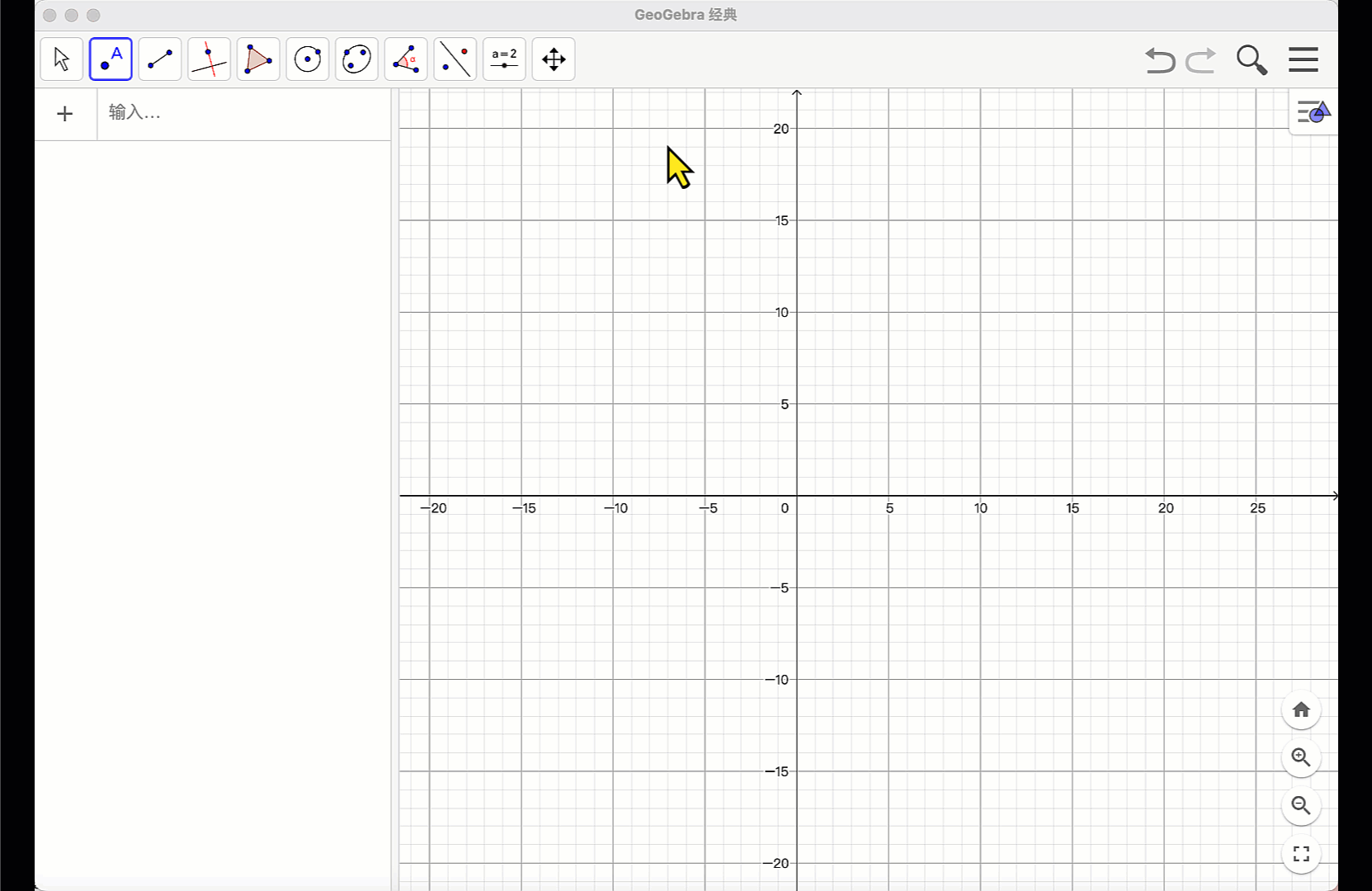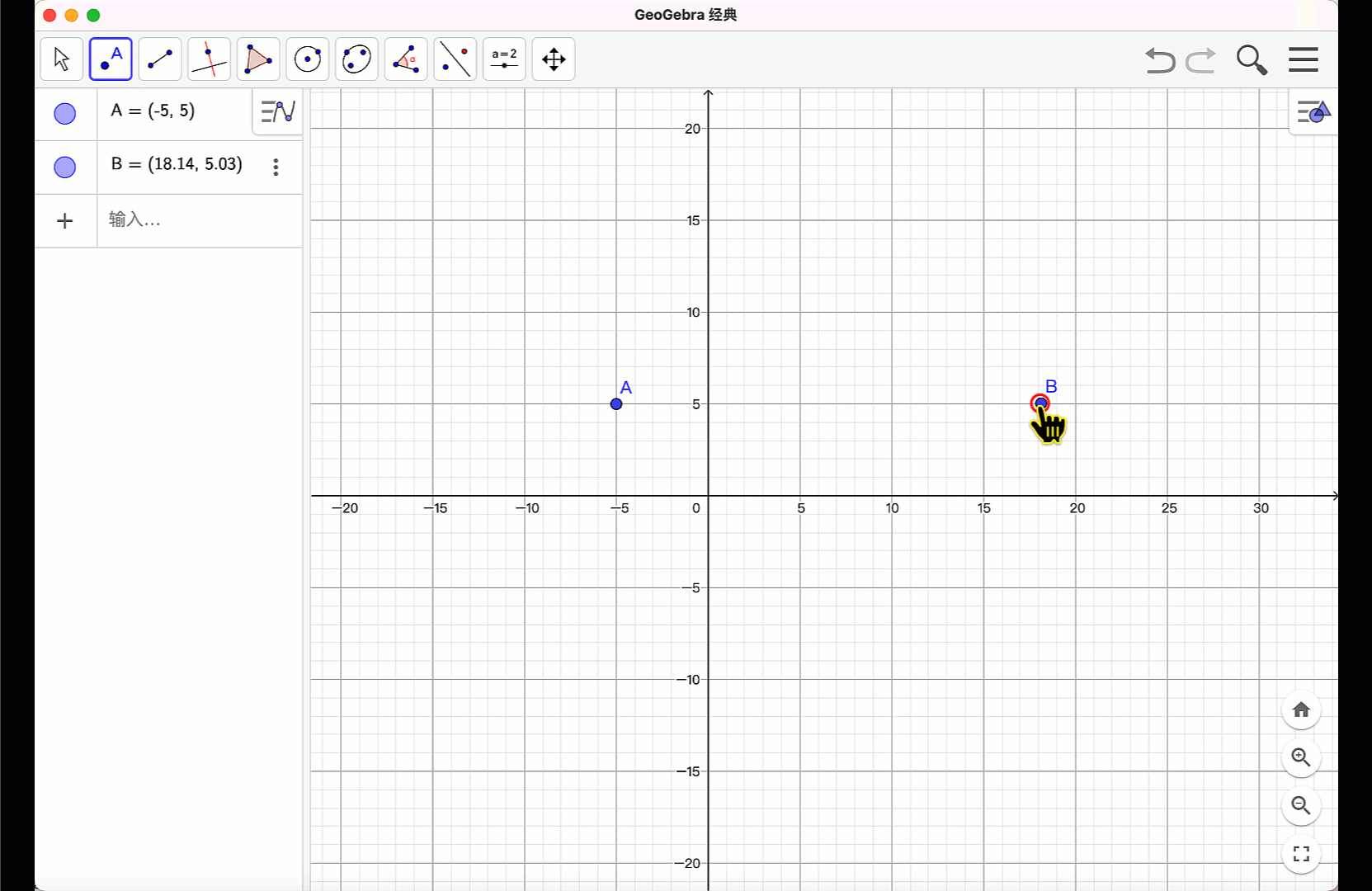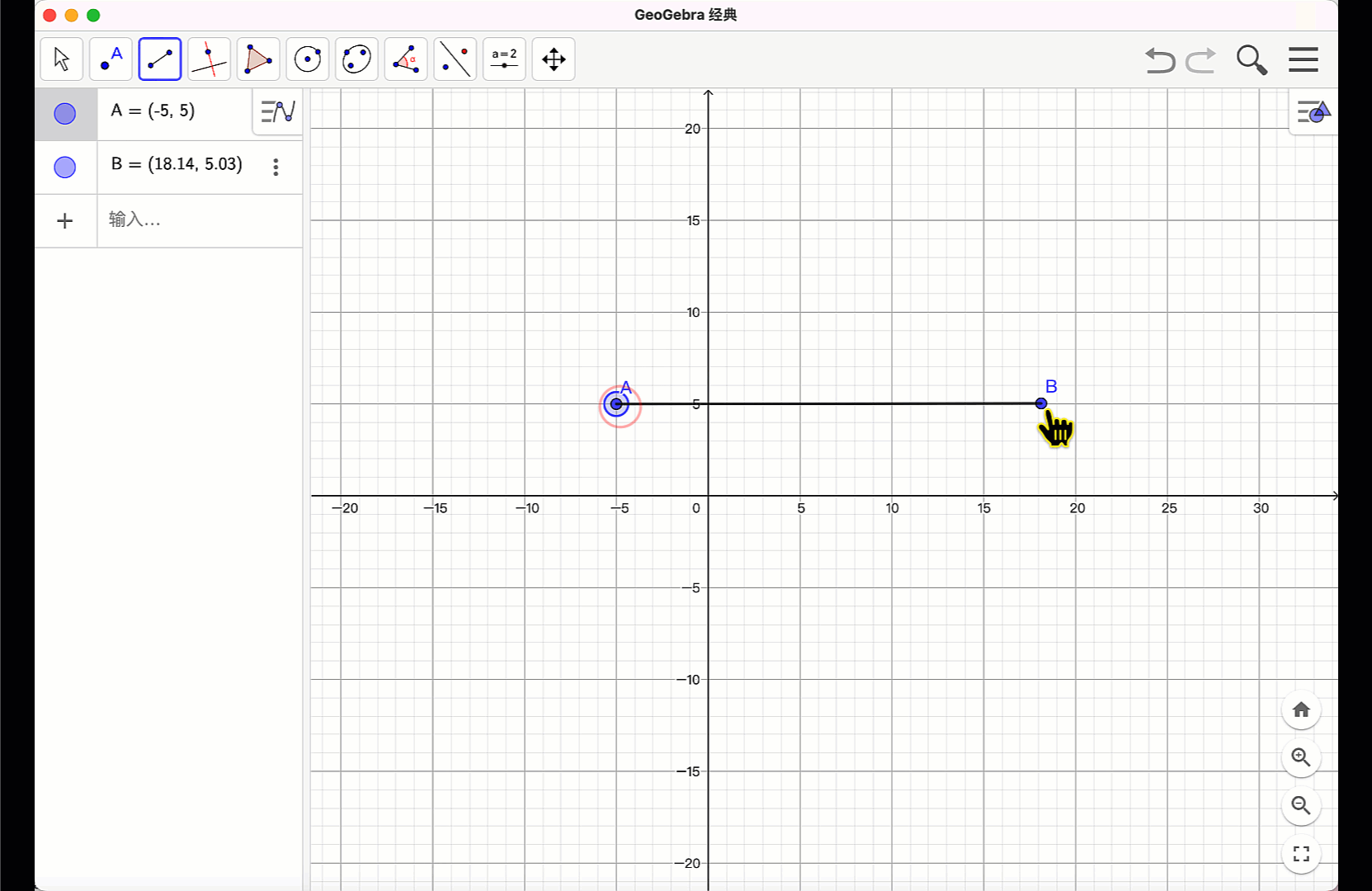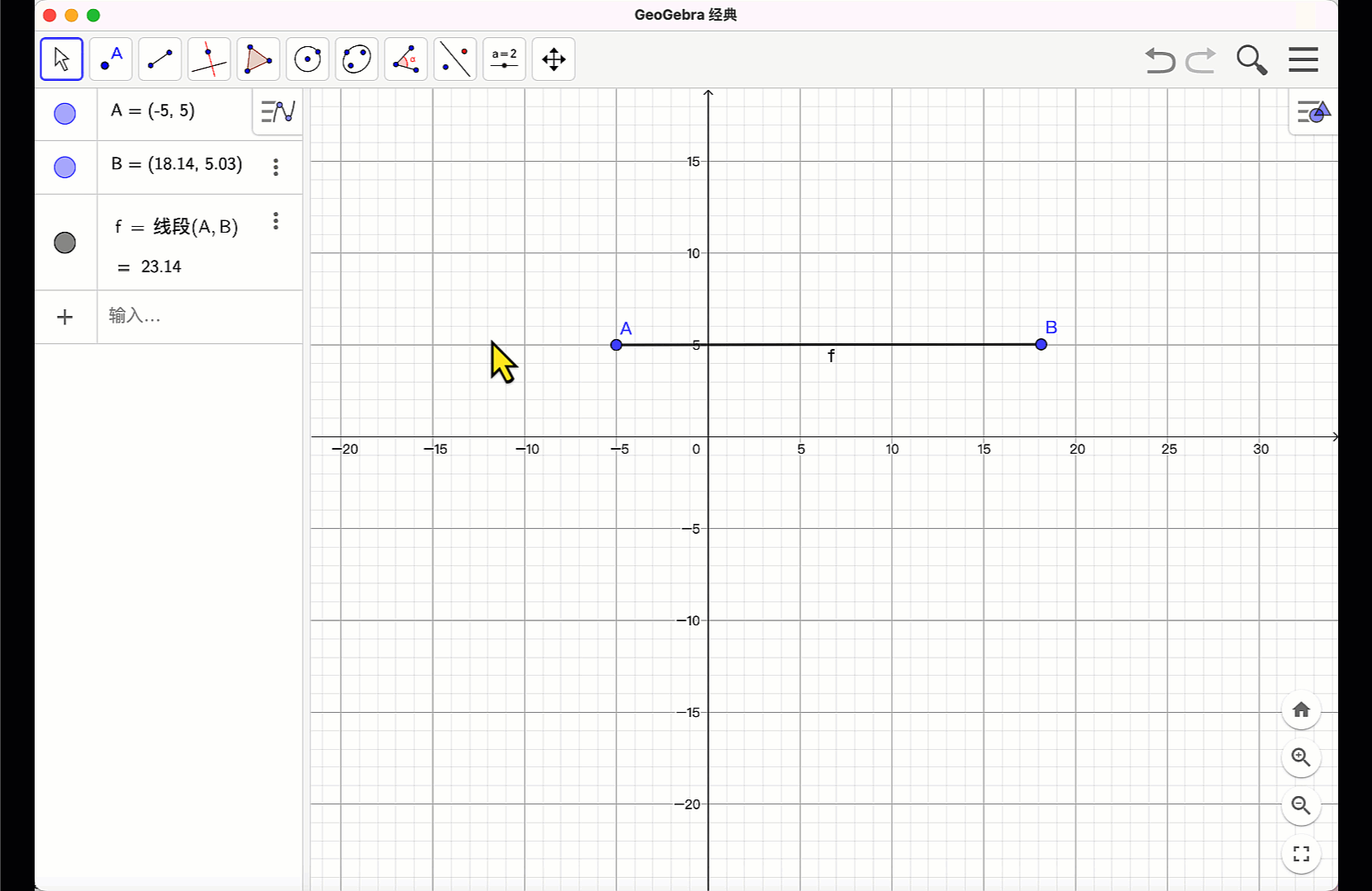
指令方式:在“指令栏”输入:”A=(3,5),B=(10,9)”。构造两个点。再输入:Segment(A,B),回车后,就在“绘图区”构造出线段AB,在“代数区”同步出现线段AB 的标签f和长度等信息。
按“Esc”键或者鼠标点“移动”工具,释放鼠标工具,拖动点A 和点B 的位置,线段的长度、位置都随之改变,代数区的信息也同步更新,体现了数形结合的动态统一。
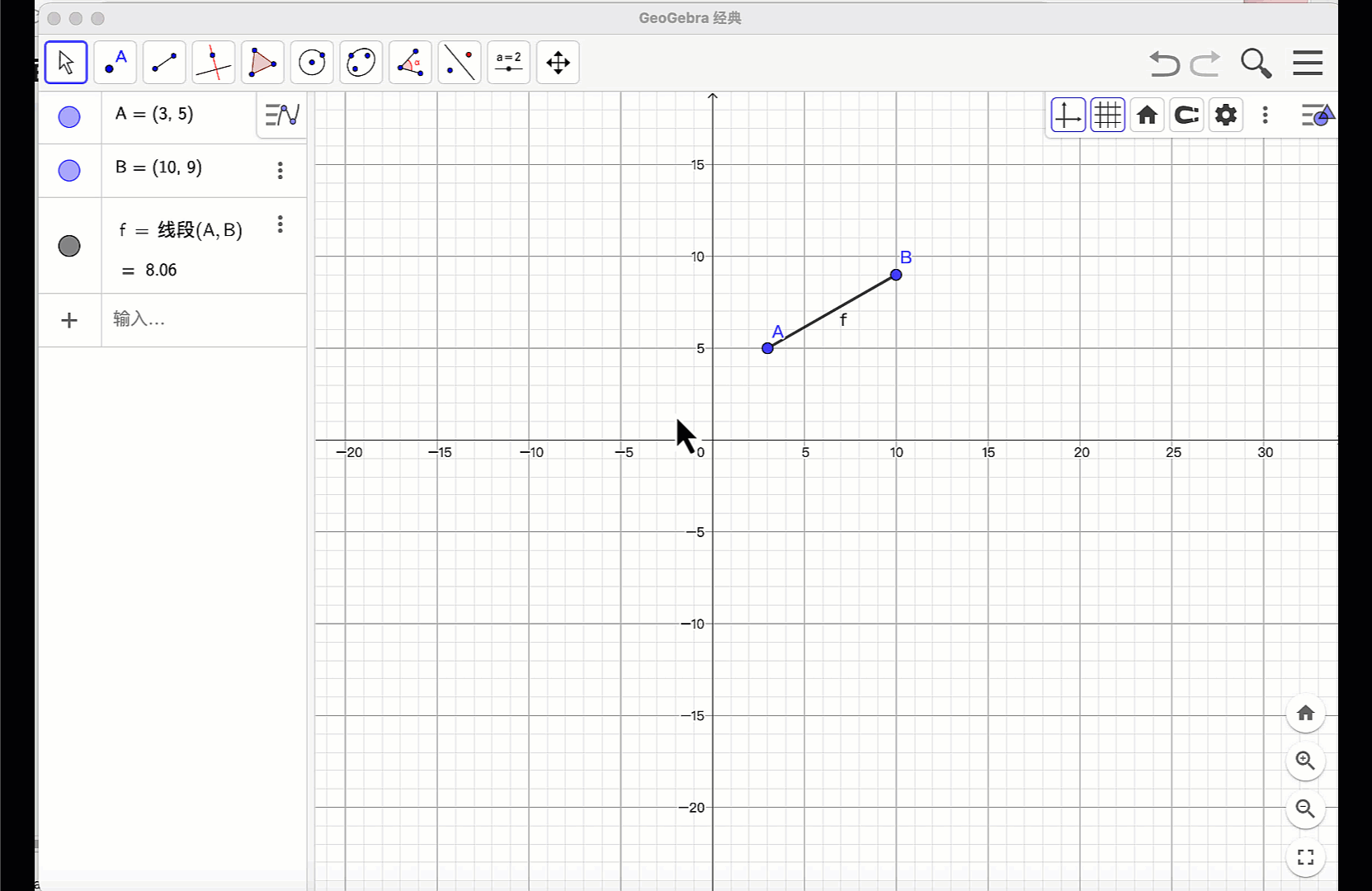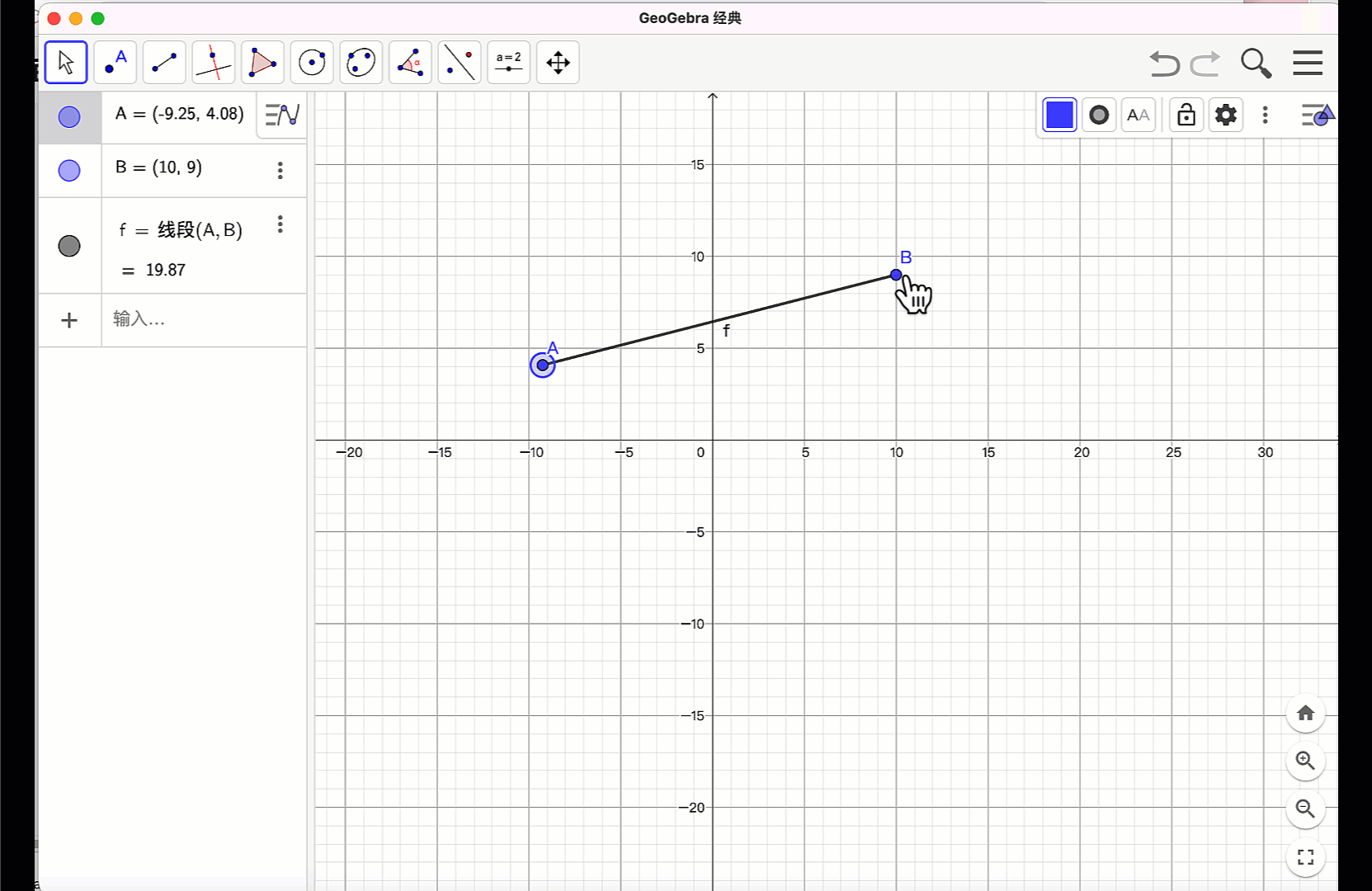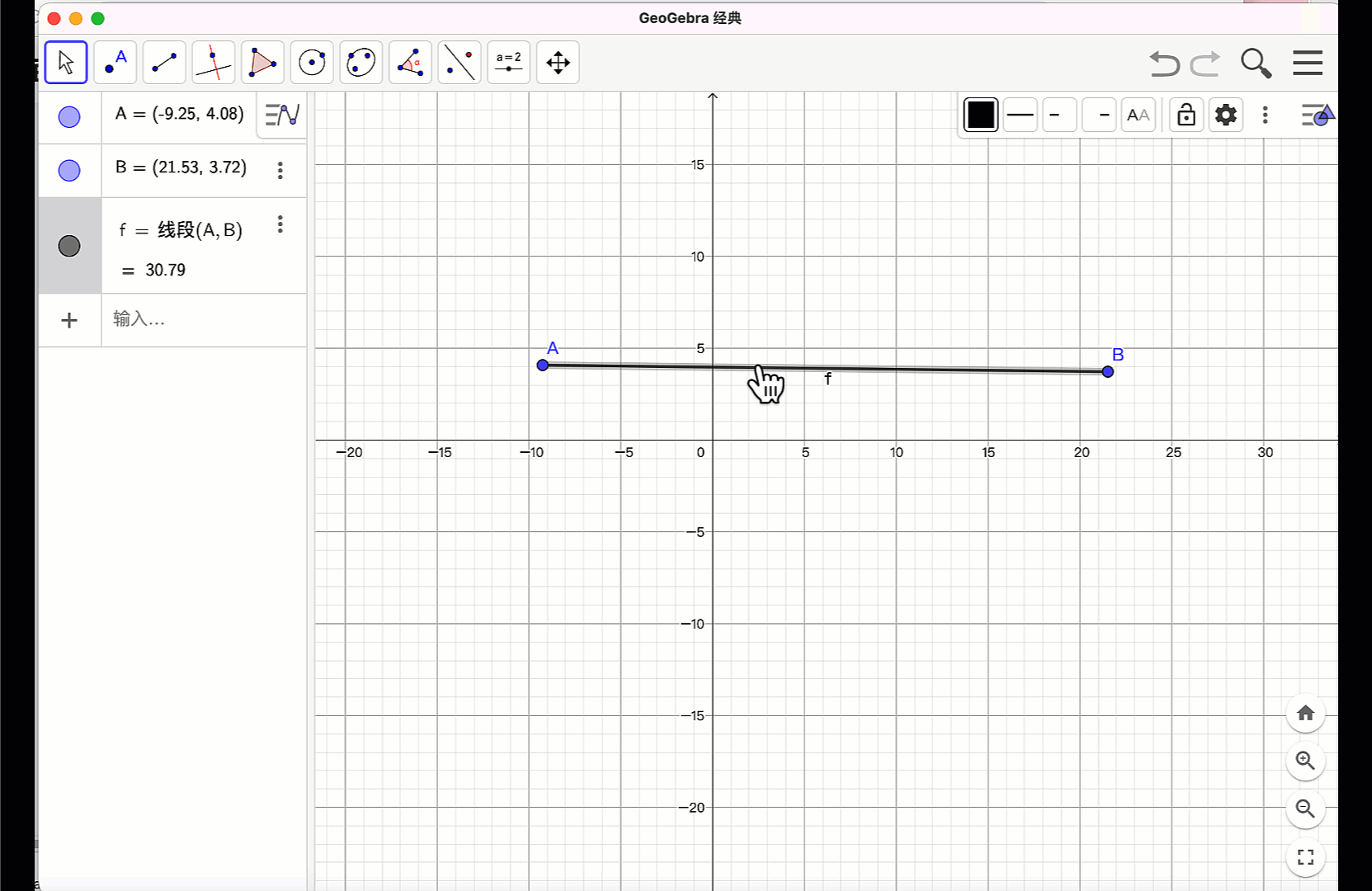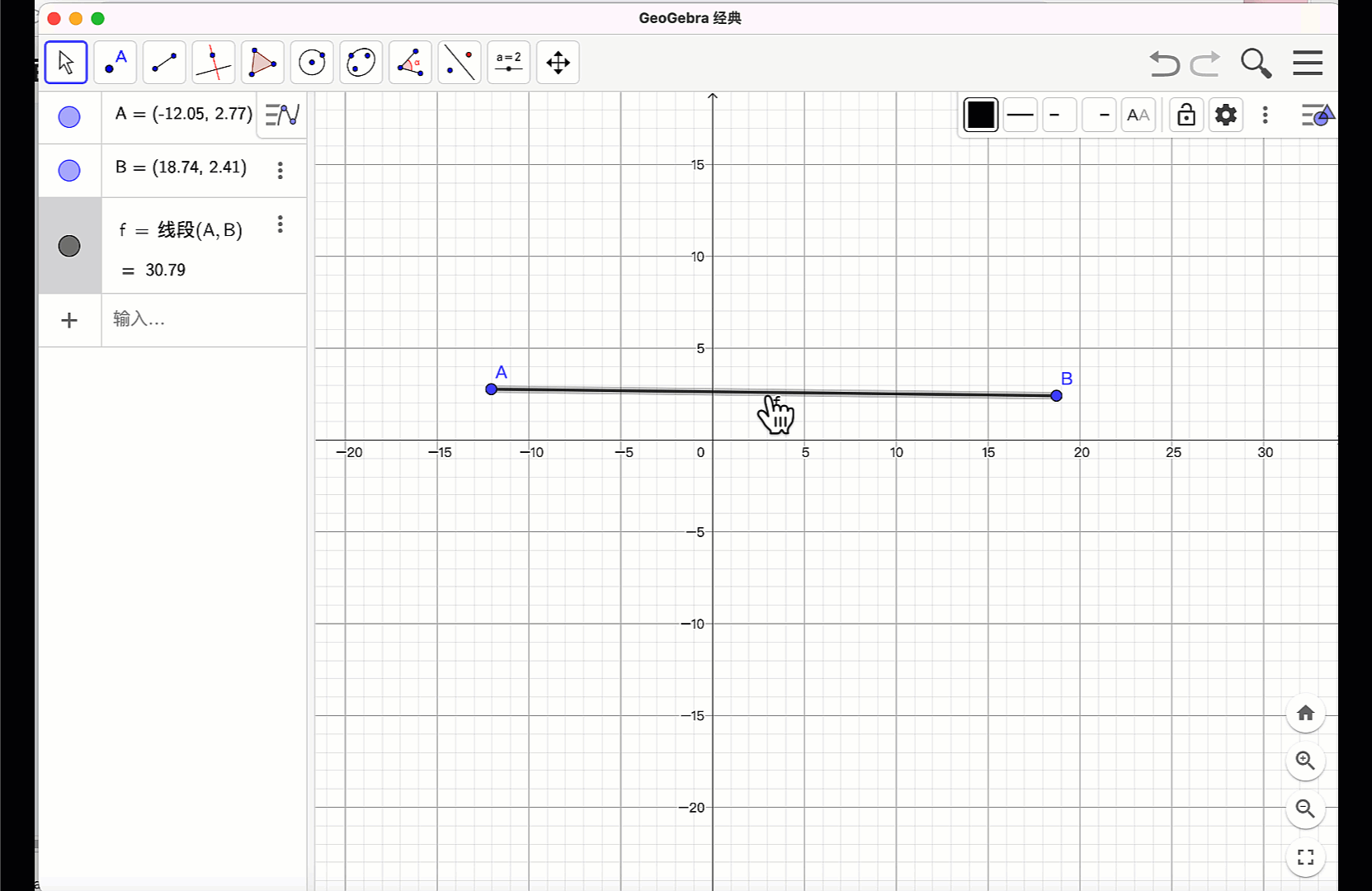
在GeoGebra中,可以多种语言。当软件界面选用了中文,就可以在指令窗口,使用中文指令和英文指令。如:构造线段,可以输入:“线段(A,B)”或者“Segment(A,B)”。但要注意的是:输入指令时使用的括弧、逗号和英文字符等都是半角英文状态。


-300x185.jpg)