斐波那契数列的python算法及其时间复杂度对比
斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,是一个著名的数列,由意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci)提出。它指的是这样一个数列:0,1,1,2,3,5,8,它从第3项开始,每一项都等于前两项之和。斐波那契数列可以通过递推的方式定义,递推公式为F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2),其中n≥2且n属于自然数集。斐波那契数列不仅在数学中有广泛的应用,还在日常生活中有许多实例,如植物的叶子排列、花朵的花瓣数量等。此外,斐波那契数列与黄金分割有密切的联系,当数列项数趋向于无穷大时,相邻两项的比值逐渐逼近黄金分割比0.618。
时间复杂度
程序的时间复杂度是用来描述程序运行时间与问题规模之间关系的指标。它帮助我们预测程序在处理不同规模数据时的大致运行时间,从而评估算法的效率。时间复杂度通常用大O符号(O)表示,例如O(n)、O(n²)等,其中n表示问题的规模。
- 常数时间复杂度 O(1):表示算法的执行时间是一个常数,不随输入规模变化。
- 对数时间复杂度: O(log n):表示算法的执行时间随着输入规模的增加而以对数方式增长。
- 线性时间复杂度: O(n):表示算法的执行时间与输入规模成线性关系。
- 平方时间复杂度: O(n²):表示算法的执行时间随输入规模的增加而呈平方级增长。
- 指数时间复杂度: O(2^n):表示算法的执行时间随输入规模的增加以指数级增长。
时间复杂度有助于选择最优算法。在面对多个解决同一问题的算法时,选择具有较低时间复杂度的算法通常能提高程序的运行效率。时间复杂度是评估算法效率的一个重要指标,但并不是唯一标准。还需要考虑空间复杂度、可读性、可维护性等因素。
查看代码运行时间的方法
Python有很多开发和调试环境可以了解代码运行时间。比如可以通过Ipython中的魔法命令%time、%timeit、%%time、%%timeit来查看,也可以通过在代码中加入time模块来计算代码运行时间 。因为两种方式的底层实现存在一定区别,所以得到的代码运行时间也不一致,举个例子。
比如计算从1到1000000(每隔3个数:1,4,7……)的平方,并输出。
方法1:在代码中引入time模块,通过比较开始和结束时两个系统时间来计算程序运行时间。

在VSCode导入Time模块实现
执行时间为0.55秒
方法2:在Ipython(现为Jupyter QtConsole)中通过魔法命令查看代码运行时间。
在提示符后输入:
%%time
test_work=[x**2 for x in range(1,1000001,3)]
print(test_work)
然后按Shift+Enter键,运行。
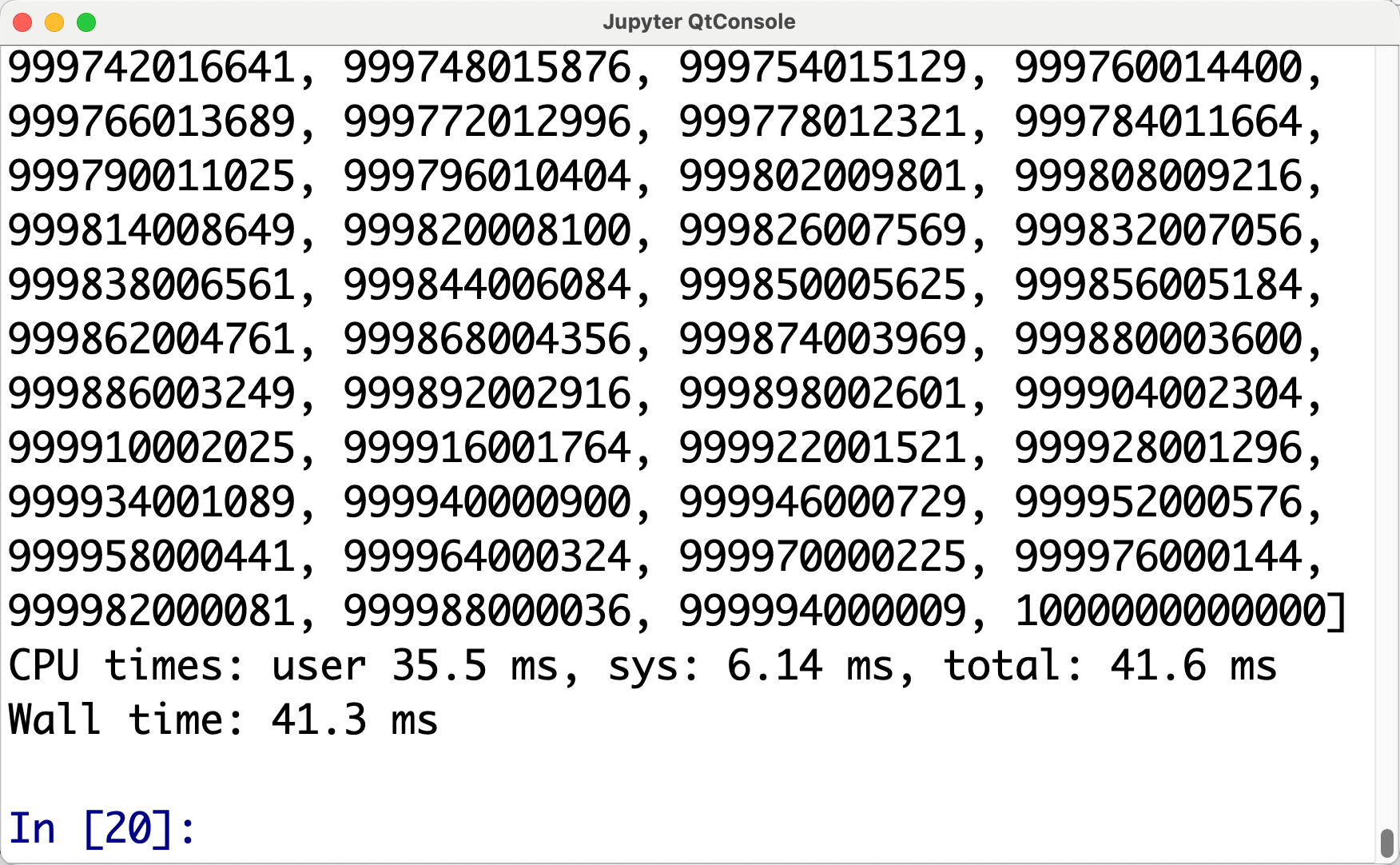
总时间为41.6ms
两种环境对比,Ipython的时间更短,两者时间相差近10倍。后面通过斐波那契数列的实现算法时间可以看出二者依然存在较大区别。
斐波那契数列的Python算法
方法1:递归调用
时间复杂度:O(2^n),因为每个斐波那契数都是前两个数的和,递归会重复计算很多相同的子问题。算法代码为:
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2) # 返回斐波那契数列第n个数。
for i in range(30): # 输出前30个数
print(fibonacci(i), end=” “)
在Ipython中输入%%time魔法命令后,接着输入以上代码,然后按Shift+Enter执行这一段代码。
得到斐波那契数列的前30个,并计算出运行时间为202ms。
运行时间为202ms
接下来看看在VSCode中的运行情况。
通过在算法前后加入如下代码实现运行时间的计算:
运行时间为3.2秒多
该算法VSCode中运行时间约是Ipython中的10倍。
方法2:递归调用(使用缓存装饰器)
Python的缓存(lru_cache)是一种装饰在被执行的函数上,将其执行的结果缓存起来,当下次请求的时候,如果请求该函数的传参未变则直接返回缓存起来的结果而不再执行函数的一种缓存装饰器。
算法代码为:
from functools import lru_cache
@lru_cache(maxsize=None) # 使用缓存装饰器,提高读取速度
def fibonacci(n):
if n <= 0:
return []
elif n == 1:
return [0]
elif n == 2:
return [0, 1]
else:
result = fibonacci(n-1)
result.append(result[-1] + result[-2])
return result
print(fibonacci(30))
Ipython中运行时间为633µs
VSCode运行时间约为0.1ms
加入Python的缓存装饰器后,无论是在Ipython还是VSCode中运行。程序运行速度都大大提升了,运行时间从毫秒缩减到微秒级了。Ipython还是比 VSCode快接近2倍。
把递归改为1000次时,Ipython依然能正确运行,时间也只是2.7ms.
在VSCode中当递归次数达到497时,只需要了1.5ms。但超过497就会报错,提示:RecursionError: maximum recursion depth exceeded 错误表示递归调用的深度超出了Python解释器所允许的最大限度。
方法3:使用Lambda和列表推导式
时间复杂度:O(n),因为列表推导式内部还是基于循环生成的。
算法代码:
def fibonacci(n):
fib = lambda x: x if x <= 1 else fib(x-1) + fib(x-2)
return [fib(i) for i in range(n)]
print(fibonacci(30))
利用lambda和列表推导式可以极大的简化代码书写。来看看输出前30个数的运行情况。
Ipython中用了219ms
VSCode中用了3秒多
时间还能接受,但当输出前50个的时候,时间就大幅度增长了。看来lambda虽然简洁,但不适合这样需要多次迭达的场景。
方法四:循环(动态)
时间复杂度:O(n),因为只需要遍历n次来生成n个斐波那契数。
利用循环通过存储中间结果来避免重复计算,是最有效的计算大量斐波那契数的方法。
算法代码:
def fibonacci(n):
if n <= 0:
return []
result = [0, 1]
for i in range(2, n):
result.append(result[i-1] + result[i-2])
return result
print(fibonacci(50))
来看看运行情况。
Ipython中用时102µs
VSCode中用时50µs
二者都非常快。提高一下难度。将个数增加到500时。
VSCode中约为830µs
利用循环方法计算列表,避免了递归中的重复计算,效率更高。
此外还有另外一种形式的循环,输出最后一个数不大于n的斐波那契数列。
def fibonacci(n):
i=0
result = []
a, b = 0, 1
while a < n:
result.append(a)
a, b = b, a + b # 先计算“=”右边的b和a+b的值,再分别赋给a,b
i=i+1#用来记录输出个数
return (result,i)
print(fibonacci(4212543535435100))
同样输出前500个数,看看这个算法中Ipython和VSCode的表现。
Ipython中用时774µs
VSCode中用时951µs
小结
递归方法对于计算大量斐波那契数(即便只有50个)可能非常慢,递归次数太多,甚至会导致栈溢出。经过对比分析,在输出斐波那契数列时,通常会使用带缓存的递归、循环(动态规划)等方法。


-300x200.jpg)

